Espacio de Lengua y Literatura de CICLO BÁSICO
Ante cualquier inconveniente, comunicarse con la docente a cargo.
robertk2santos.milaulas.com
-
Bienvenido a su nuevo sitio en Mil Aulas
¡Ya puede empezar a crear cursos!
Moodle es un sistema de gestión de aprendizaje de código abierto que permite a los educadores crear y administrar cursos en línea. Ofrece una variedad de herramientas y recursos para organizar el material del curso, crear actividades y cuestionarios, alojar discusiones en línea y hacer un seguimiento del progreso de los estudiantes.
La plataforma es altamente personalizable y puede adaptarse a las necesidades específicas de cada institución o curso. Esto significa que los educadores pueden crear cursos que se ajusten a sus objetivos y metodologías, y personalizarlos para el aprendizaje de cada estudiante. Moodle también admite tanto entornos de aprendizaje síncronos como asíncronos, lo que permite a los educadores organizar eventos en vivo y proporcionar recursos para el aprendizaje a su propio ritmo.
Moodle es ampliamente utilizado en instituciones educativas de todo el mundo, desde escuelas primarias hasta universidades. También es popular en programas de formación profesional y empresarial. Además, la plataforma es accesible para usuarios de diferentes habilidades y necesidades, lo que la hace inclusiva para todos los estudiantes.
La comunidad de Moodle es activa y diversa, compuesta por educadores, desarrolladores y usuarios de todo el mundo. La comunidad contribuye al desarrollo y mejora continua de Moodle, y proporciona soporte, recursos y documentación para los usuarios. La plataforma también ofrece una gran cantidad de recursos y herramientas para mejorar la experiencia de los usuarios y fomentar la colaboración y el aprendizaje interactivo.
Enlaces de interés:
- Documentación oficial de Moodle
- Foros de la comunidad Moodle
- Historial de versiones de Moodle (En inglés)
- El servicio de alojamiento gratuito de Moodle en Mil Aulas
(Puede editar o eliminar este texto)
Cursos disponibles
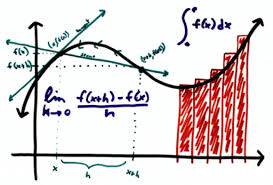
Análisis Matemático II: Explorando la Dinámica del Cambio
Este curso de Análisis Matemático II está diseñado para estudiantes de secundaria técnica y se enfoca en proporcionar una comprensión sólida y aplicada de los conceptos fundamentales del cálculo diferencial e integral. El objetivo principal es equipar a los estudiantes con herramientas matemáticas esenciales para el análisis de problemas técnicos y científicos, permitiéndoles modelar, predecir y optimizar fenómenos que involucran el cambio.
El programa se estructura en tres ejes principales, progresando desde la comprensión del comportamiento local de las funciones hasta el estudio de la acumulación y las tasas de variación:
1. Límite y Continuidad de Funciones
Este eje sienta las bases del cálculo. Exploraremos cómo se comporta una función en las proximidades de un punto específico, introduciendo el concepto de límite. Se analizará la continuidad de funciones, que es crucial para garantizar que los modelos matemáticos sean representaciones coherentes de los fenómenos físicos o técnicos. Se prestará especial atención a la identificación de discontinuidades y a la interpretación de los límites infinitos y al infinito.
-
Conceptos Clave: Noción intuitiva y formal del límite, límites laterales, asíntotas verticales y horizontales, definición de continuidad, tipos de discontinuidades.
-
Aplicación Técnica: Análisis de la estabilidad de un sistema o circuito al aproximarse a un valor crítico.
2. Derivadas: La Razón de Cambio Instantánea
El concepto de derivada es la herramienta central para medir la tasa de cambio instantánea de una función. En este eje, estudiaremos cómo calcular las derivadas de diversas funciones (polinómicas, trigonométricas, exponenciales, etc.) y las reglas fundamentales de la derivación. Las derivadas se aplicarán para resolver problemas de optimización (maximizar beneficios, minimizar costos) y para analizar el comportamiento local de las funciones, como la determinación de pendientes, velocidades, aceleraciones, puntos críticos e intervalos de crecimiento/decrecimiento.
-
Conceptos Clave: Definición de derivada como límite, reglas de derivación (suma, producto, cociente, cadena), derivada de orden superior, diferenciación implícita, el Teorema de L'Hôpital, máximos y mínimos.
-
Aplicación Técnica: Cálculo de la velocidad instantánea en un proceso productivo, diseño para la eficiencia máxima de un componente, análisis de la pendiente de una trayectoria o curva técnica.
3. Integrales: Acumulación y Áreas
El último eje introduce el cálculo integral, que se enfoca en la noción de acumulación y el cálculo de áreas bajo una curva. Se explorará la integral definida para calcular el área y la integral indefinida (antiderivada). El vínculo fundamental entre la derivada y la integral se establecerá a través del Teorema Fundamental del Cálculo. Se aplicarán técnicas de integración para resolver problemas relacionados con el volumen, el trabajo y el valor promedio de una función.